局所一様媒質に対する Volume Rendering 方程式の漸化式
December 16, 2021
これは レイトレ Advent Calendar 2021 の記事です.
はじめに #
リアルアイムレンダリングの話をします.
[ Hillaire 2016] の 5.6.3 節では, 散乱媒質を描画するときに, Volume Rendering 方程式の内部散乱項に対して入射光と散乱媒質を一様としたときに得られる, 解析解を利用しています.
後に述べるように, この解析解は 指数フォグを一般化したものに相当します.
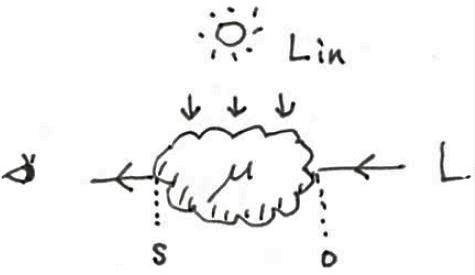
解析解には, 数値積分の誤差が生じません. このため, レイマーチング[ Wrenninge and Zafar 2011]などによって散乱媒質を描画するとき, 入射光と散乱媒質が局所的に一様とみなせるところで, その計算精度を改善してくれます.
ただし [ Hillaire 2016] で行われている議論は, ひとつの散乱媒質と単一散乱に絞ったものです. より一般的な議論を行うためには, 複数の散乱媒質と多重散乱を含んだものを, Volume Rendering 方程式から明示的に求めた資料が欲しいところです.
そこで, この記事では複数媒質の Volume Rendering 方程式から出発して, 入射光と散乱媒質を局所的に一様としたときの漸化式を導きます1.
複数媒質の Volume Rendering 方程式 #
まずは, Volume Rendering 方程式を導入します.
Volume Rendering 方程式とは, 散乱媒質内を進行する光の輝度の変化を記述する方程式で, 文献によっては Radiative Transfer 方程式とも呼ばれます. この記事では, 時間に依存しない Radiative Transfer 方程式を Volume Rendering 方程式と呼びます2.
ただし, その導出の詳細3には触れず, 現象論的な導入 [ Arvo. 1993] [ Fong et al. 2017] [ Novák et al. 2018] のみをおさらいします. また, この記事では, レイリー散乱とミー散乱をする2種類の媒質を混ぜて扱えるように, 複数の散乱媒質に対する Volume Rendering 方程式を導入します.
散乱媒質と光 #
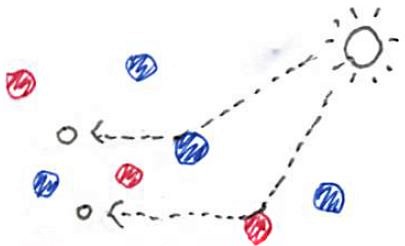
白丸:フォトン, 赤:1種類めの散乱媒質, 青:2種類めの散乱媒質
空気中のちりを \(I\) 種類の散乱体からなる粒子の集団, そして空間を進む光を光子からなる粒子の集団であると簡略化4します. そして, 散乱体の集団を「散乱媒質」, 光子の集団を「フォトン」と呼ぶことにします5. 簡単のため, 粒子の形状は全て球とします.
Volume Rendering 方程式に進む準備として, フォトンの密度を表す輝度と, 散乱媒質の密度を表す散乱係数, そして散乱媒質によるフォトンの散乱を表す位相関数を導入します.
輝度 #
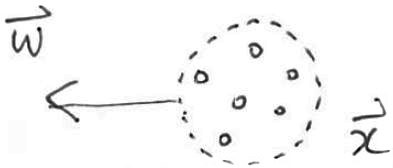
フォトンの密度は, 位置 \(\bm{x}\) と方向 \(\bm{\omega}\) に対する輝度 \(L(\bm{x},\bm{\omega})\) で表します.
散乱係数 #
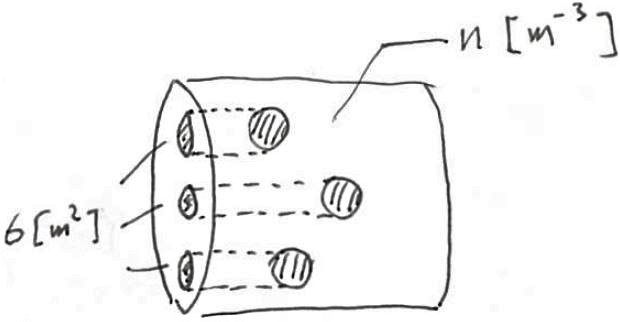
ある方向から \(i\) 種類めの散乱体を眺めたときの断面積を散乱断面積 \(\sigma^{(i)}\) と呼び, その散乱体の個数密度を \(n^{(i)}(\bm{x})\) とします. このとき, 単位体積当たりの散乱断面積を散乱係数 \(\mu^{(i)}_s(\bm{x}):=\sigma^{(i)}n^{(i)}(\bm{x})\) で表します.
散乱の位相関数 #
散乱体の性質に応じて, 光との相互作用は単に弾性散乱を考えるだけで良い場合もあれば, 電磁波の散乱を考慮する必要がある場合もあります.
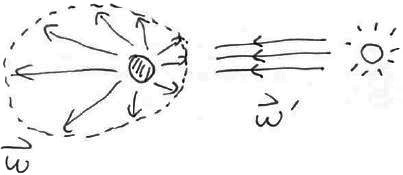
そこで, \(i\) 種類めの散乱媒質が, 方向 \(\bm{\omega}'\) から来たフォトンを方向 \(\bm{\omega}\) に散乱する割合を 位相関数 \(p^{(i)}(\bm{\omega},\bm{\omega}')\) と書き, その中に様々な効果によって起こる散乱の方向分布を埋め込むことにします.
なお, 位相関数は, 球面上で積分したときに 1 となるように規格化されています. \[\begin{aligned} \int_{\bm{\omega}'\in\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}')d\bm{\omega}' = 1 \end{aligned}\]
光の吸収と放出 #
散乱媒質はフォトンを吸収する場合もあるとして, 吸収係数 \(\mu^{(i)}_a(\bm{x})\) を考えます. 散乱係数と吸収係数を合算したものを, 消散係数 \(\mu^{(i)}_e(\bm{x}) = \mu^{(i)}_s(\bm{x}) + \mu^{(i)}_a(\bm{x})\) と呼びます.
そして, フォトンの放出は source 項 \(S^{(i)}(\bm{x})\) で表します6.
Volume Rendering 方程式 #
このようにしてフォトンと散乱媒質を表現したとき, 散乱媒質中を進行するフォトンの輝度の変化は, 次の Volume Rendering 方程式で記述されます.
ただし \[\begin{aligned} \lambda^{(i)}(\bm{x},\bm{\omega}) := S^{(i)}(\bm{x},\bm{\omega}) + \mu_s^{(i)}(\bm{x}) \int_{\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}')L(\bm{x},\bm{\omega}')d\bm{\omega}' \end{aligned}\] です.Volume Rendering 方程式
\[\begin{aligned} (\bm{\omega}\cdot\nabla)L(\bm{x},\bm{\omega}) = \sum^I_i\left[\lambda^{(i)}(\bm{x},\bm{\omega}) - \mu_e^{(i)}(\bm{x})L(\bm{x},\bm{\omega})\right] \end{aligned}\]
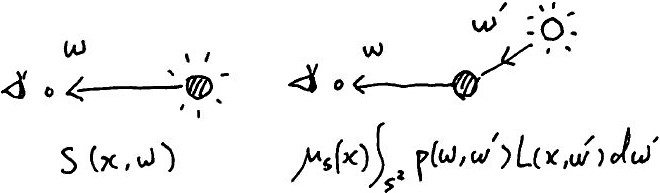
Fig. gain 項の各項
右辺の \(\lambda^{(i)}(\bm{x},\bm{\omega})\) は, source 項 \(S^{(i)}(\bm{x},\bm{\omega})\) と 内部散乱項 \(\mu_s^{(i)}(\bm{x}) \int_{\mathcal{S}^2}p^{(i)}(\bm{\omega},\bm{\omega}')L(\bm{x},\bm{\omega}')d\bm{\omega}'\) による輝度の増加を表します. この記事では, この項を gain 項と呼びます.
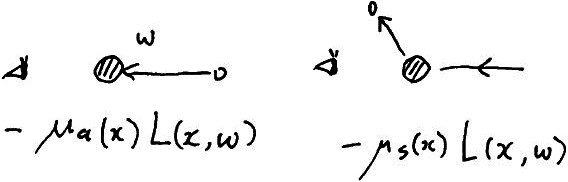
Fig. loss 項 \(-\mu_eL = -(\mu_a+\mu_s)L\)
右辺の \(\mu_e^{(i)}(\bm{x})L(\bm{x},\bm{\omega})\) は, 媒質に衝突して失われる輝度の減少を表します. この記事では, この項を loss 項と呼びます.
そして, 左辺の方向微分 \((\bm{\omega}\cdot\nabla)L(\bm{x},\bm{\omega})\) によって, 散乱媒質中を進行するフォトンの輝度の変化を表します.
Volume Rendering 方程式の積分形 #
輝度 \(L(\bm{x},\bm{\omega})\) を求めるため, Volume Rendering 方程式の積分形を考えます. 方向 \(\bm{\omega}\) に沿った積分をわかりやすくするために, 距離 \(s\) を使って位置 \(\bm{x}\) を \(\bm{x}(s)=\bm{x}(0)+\bm{\omega}s\) と表し, 方向微分を \(\left(\bm{\omega}\cdot\nabla\right)L\left(\bm{x},\bm{\omega}\right) = \frac{dL\left(\bm{x}(s),\bm{\omega}\right)}{ds}\) と書き換えます7.
すると Volume Rendering 方程式は \[\begin{aligned} \frac{dL\left(s,\,\bm{\omega}\right)}{ds} = \sum^I_i\left[\lambda^{(i)}(s,\,\bm{\omega}) - \mu^{(i)}_e(s)L\left(s,\,\bm{\omega}\right)\right] \end{aligned}\] となります. ここで \(L(\bm{x}(s),\bm{\omega})\) を \(L(s,\bm{\omega})\) と略記しました. \(\lambda^{(i)}(s,\bm{\omega})\) や \(\mu^{(i)}_e(s)\) も同様です.
上式は一階線形微分方程式なので, その積分形は次のように求まります8
ただし \[ \begin{aligned} \tau(a,b) &:= \exp\left[-\int^b_{s''=a}\left(\sum^I_i\mu_e^{(i)}(s'')\right)ds''\right]\\ \lambda(s',\bm{\omega}) &:= \sum_i\left[S^{(i)}(s',\bm{\omega}) + \mu_s^{(i)}(s') \int_{\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}')L(s',\bm{\omega}')d\bm{\omega}'\right] \end{aligned}\] です. ここで導入した \(\tau(a,b)\) を transmittance と呼びます.Volume Rendering 方程式(積分形)
\[ \begin{aligned} L(s,\bm{\omega}) =L\left(0,\bm{\omega}\right)\tau(0,s) + \int^s_{s'=0}\lambda(s',\bm{\omega})\tau(s',s) ds' \end{aligned}\]
以上により, 位置 \(\bm{x}(0)\) で輝度 \(L(0,\bm{\omega})\) を持つ物体を 位置 \(\bm{x}(s)\) から眺めたときの輝度 \(L(s,\bm{\omega})\) は, Volume Rendering 方程式を解けば求まることがわかりました.
ただし, 内部散乱項に対する入射光 \(L(s', \bm{\omega}')\) は, どこかの光源から直接来たフォトン \(L^{\text{0th}}\) のほか, 他の物体に1回散乱してから来たフォトン \(L^{\text{1st}}\) や 2回散乱して来たフォトン \(L^{\text{2nd}}\) .. などと 媒質に繰り返し散乱してから来たフォトンを含んでいます.
\[ \begin{aligned} u_s^{(i)}(s')\int_{\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}') \left[L^{\text{0th}}(s',\bm{\omega}') + L^{\text{1st}}(s',\bm{\omega}') + L^{\text{2nd}}(s',\bm{\omega}') + \cdots\right] d\bm{\omega}'\\ \end{aligned}\]これらのフォトンの輝度もまた, Volume Rendering 方程式によって解かれていなければならないため, この方程式は簡単に解くことはできません. この問題は, モンテカルロ法を用いて 多数のフォトンの経路に沿って Volume Rendering 方程式を再帰的に解き, 輝度 \(L(s,\bm{\omega})\) の期待値を求めることで 解決できることが知られています9.
一方, リアルタイムレンダリングでは一般的に, 散乱の高次項をさまざまな近似手法で取り扱います. この記事ではその詳細には触れず, 単に入射光が直接光 \(L_{\text{in}}^{\text{direct}}\) と間接光 \(L_{\text{in}}^{\text{indirect}}\) で書けるとしておきます.
\[ \begin{aligned} u_s^{(i)}(s')\int_{\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}') L_{\text{in}}(s',\bm{\omega}') d\bm{\omega}' \end{aligned}\] \[ \begin{aligned} L_{\text{in}}(s',\bm{\omega}') &= L_{\text{in}}^{\text{direct}}(s',\bm{\omega}') + L_{\text{in}}^{\text{indirect}}(s'\bm{\omega}')\\ L_{\text{in}}^{\text{direct}}(s',\bm{\omega}') &:= L^{\text{0th}}(s',\bm{\omega}')\\ L_{\text{in}}^{\text{indirect}}(s',\bm{\omega}') &:= L^{\text{1st}}(s',\bm{\omega}') + L^{\text{2nd}}(s',\bm{\omega}') + \cdots \end{aligned}\]
ここで, 内部散乱項に対する入射光を明示するため, \(L(s',\bm{\omega}')\) を \(L_{\text{in}}(s',\bm{\omega}')\) と書きました.
局所的に一様な媒質に対する漸化式 #
この節では, レイマーチング[ Wrenninge and Zafar 2011]やボリュームフォグ[ Wronski 2014]といった手法を導くことを念頭に置いて, 視点 \(\bm{x}(s_e)\) ともう一方の端点 \(\bm{x}(s_s)\) の間を \(N\) 個の区間に分割し, その区間に沿って Volume Rendering 方程式を繰り返し解くことを考えます.
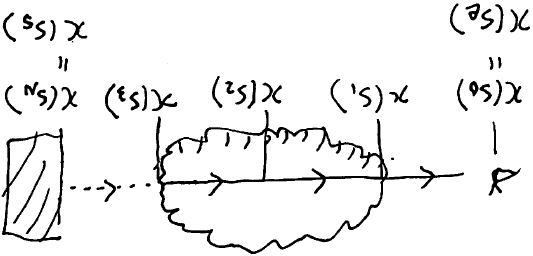
局所的に一様な媒質 #
いま, Volume Rendering 方程式を1ステップ計算するあいだ, 散乱媒質と入射光が局所的に一様であると仮定します10.
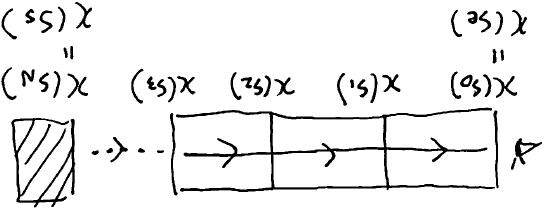
以下で, その各ステップの積分が解析的に解けることを示します.
解析解 #
散乱係数と入射光が一様, すなわち \(\bm{x}\) に依存しないとき, Volume Rendering 方程式は次のように書けます. \[\begin{aligned} L(s_n,\bm{\omega}) = L\left(s_{n-1},\bm{\omega}\right)\tau(s_{n-1},s_n) + \int^{s_n}_{s'=s_{n-1}}\lambda(\bm{\omega})\tau(s',s_n) ds' \end{aligned}\] \[\begin{aligned} &\tau(a,b) :=\exp\left[-\left(\sum^I_i\mu^{(i)}_e\right)|b-a|\right]\\ &\lambda(\bm{\omega}) := \sum^I_i\left[ S^{(i)}(\bm{\omega}) + \mu^{(i)}_s \int_{\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}')L_{\text{in}}(\bm{\omega}')d\bm{\omega}' \right] \end{aligned}\]
このとき, 次の項は解析的に解けます. \[\begin{aligned} \int^{s_n}_{s'=s_{n-1}}\lambda(\bm{\omega})\tau(s',s_n) ds' &= \int^{s_n}_{s'=s_{n-1}}\lambda(\bm{\omega})e^{-\left(\sum^I_i\mu^{(i)}_e\right)(s_n-s')} ds'\\ &= \lambda(\bm{\omega}) e^{-\left(\sum^I_i\mu^{(i)}_e\right)s_n}\int^{s_n}_{s'=s_{n-1}}e^{\left(\sum^I_i\mu^{(i)}_e\right)s'} ds'\\ &= \frac{\lambda(\bm{\omega})}{\sum^I_i\mu^{(i)}_e}\left[1-\tau(s_{n-1},s_n)\right] \end{aligned}\]
これにより, Volume Rendering 方程式の解析解が次のように得られます.
Volume Rendering 方程式の解析解
\[\begin{aligned} L(s_n,\bm{\omega}) = L\left(s_{n-1}, \bm{\omega}\right)\tau(s_{n-1}, s_n) + \frac{\lambda(\bm{\omega})}{\sum^I_i\mu^{(i)}_e}\left[1-\tau(s_{n-1}, s_n)\right] \end{aligned}\]
こうして, [ Hillaire 2016] の 5.6.3 節で 示されている解析解を一般化したものが得られました. この式は \(\tau(s_{n-1}, s_n)\) をアルファとする, 単純なアルファブレンドの形になっていることも特筆すべきところです.
なお, 上式で吸収係数 \(\mu^{(i)}_a\) と source 項 \(S^{(i)}(\bm{\omega})\) をゼロ, そして位相関数を等方 \(p^{(i)}(\bm{\omega},\bm{\omega}')=\frac{1}{4\pi}\), 入射光も等方 \(L_{\text{in}}(\bm{\omega}')=L_{\text{in}}\) としたとき, はじめにで取り上げた 指数フォグ
指数フォグ
\[\begin{aligned} L(s_n,\bm{\omega}) = L(s_{n-1},\bm{\omega})e^{-\mu_s |s_n-s_{n-1}|} + L_{\text{in}}(1-e^{-\mu_s |s_n-s_{n-1}|}) \end{aligned}\]
が得られます11. 以後, ひとつの距離に基づいて散乱媒質の計算を行う手法を, 距離ベースのフォグ [ Wenzel 2007]と呼びます.
漸化式 #
Volume Rendering 方程式の解析解を次々に解くために, 次のような表記を行います. \[ \begin{aligned} L_n:=L(s_n,\bm{\omega}),\quad t_n:=\tau(s_{n-1}, s_n),\quad l_n:= \frac{\lambda(\bm{\omega})}{\sum^I_i\mu^{(i)}_e}(1-t_n) \end{aligned}\]
この表記のもとで, Volume Rendering 方程式の解析解 は以下のように書けます
\[ \begin{aligned} L_n =L_{n-1}t_n + l_n \end{aligned}\]これを使い, \(\bm{x}(s_s)\) に輝度 \(L_s\) の物体があり, それを 視点 \(\bm{x}(s_e)\) から眺めたときの輝度 \(L_e\) を \(N\) ステップの計算で求めることを考えます. このとき, 計算は \(\bm{x}(s_s)\) から \(\bm{x}(s_e)\) に向かって行うことにします12.
まず, \(\bm{x}(s_s)\) を1ステップ手前から眺めたときの輝度 \(L_e\) は
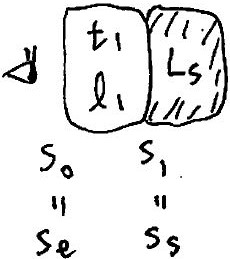
\[ \begin{aligned} L_e=L_st_1+l_1 \end{aligned}\] と求まります. そして, 2ステップ手前から眺めたときの輝度 \(L_e\) は,
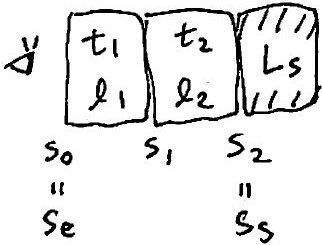
\[ \begin{aligned} L_e=L_st_2t_1 + l_2t_1 + l_1 \end{aligned}\] となります. これを \(N\) 回繰り返すと, \(L_e\) は
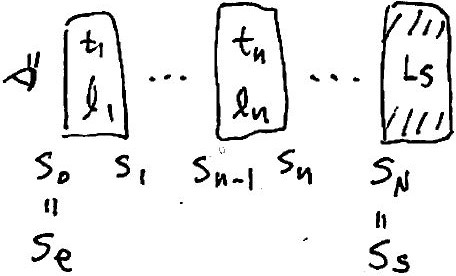
\[ \begin{aligned} L_e=L_sT_N + L_N \end{aligned}\] \[ \begin{aligned} T_n:=T_{n-1}t_n,\quad L_n:=l_nT_{n-1} + L_{n-1} \end{aligned}\] という漸化式として得られます.
まとめ #
こうして, 位置 \(\bm{x}(s_s)\) で輝度 \(L_s\) をもつ物体を, 散乱媒質を通して方向 \(\bm{\omega}\) から眺めたとき, 視点 \(\bm{x}(s_e)\) に到達するフォトンの輝度 \(L_e\) は, 次の漸化式によって与えられることがわかりました.
漸化式
\[ \begin{aligned} L_e=L_sT_N + L_N \end{aligned}\] \[ \begin{aligned} T_n:=T_{n-1}t_n,\quad L_n:=l_nT_{n-1} + L_{n-1} \end{aligned}\]
その1ステップで計算される \(t_n\) と \(l_n\) は, 次のように与えられます. \[ \begin{aligned} t_n:=e^{-\left[\sum^I_i\mu^{(i)}_e\right] |s_n-s_{n-1}|},\quad l_n:= \frac{\lambda(\bm{\omega})}{\sum^I_i\mu^{(i)}_e}(1-t_n) \end{aligned}\] \[\begin{aligned} \lambda(\bm{\omega}) := \sum^I_i\left[ S^{(i)}(\bm{\omega}) + \mu^{(i)}_s \int_{\mathcal{S}^2} p^{(i)}(\bm{\omega},\bm{\omega}') \left(L_{\text{in}}^{\text{direct}}(\bm{\omega}') + L_{\text{in}}^{\text{indirect}}(\bm{\omega}')\right) d\bm{\omega}' \right] \end{aligned}\]
漸化式の考察 #
前節で求めた 漸化式を使うことで, ステップ数を \(N=1\) とすれば距離ベースのフォグ, \(N\gt1\) とすれば, レイマーチングの積分の1ステップが得られます. \(T_n\) と \(L_n\) を3Dテクスチャのボクセルに保管すれば, それはボリュームフォグとなります.
また, 漸化式 は \(T_N\) をアルファとする pre-multiplied アルファブレンド の形になっています. これは, 2つの独立なレイマーチングによって \(T_M, L_M\) と \(T_N, L_N\) が得られたとしたとき, これらもまた同じ漸化式で合成できることを意味しています. この性質は, 例えば近景でボリュームフォグ、遠景でレイマーチングと別々に計算した結果を, 後で合成するといった用途に使えるでしょう.
さいごに #
この記事では, 複数媒質の Volume Rendering 方程式に対し, 入射光と散乱媒質が局所的に一様な場合の 解析解を求め, その 漸化式を導出しました. そして, 漸化式の考察で, それが距離ベースのフォグ同士, あるいは pre-multiplied アルファによる半透明物体同士の連結を一般化した概念になっていることがわかりました.
指数フォグの導出例で見たように, この漸化式に散乱媒質や光源を与えることで, その具体的な実装を導くことができます.
リアルタイムレンダリングの散乱媒質の計算について, どのような手法を組み合わせ, どのような媒質や光源を与え, そしてどのような近似を取るかを議論するとき, この記事が参考になれば幸いです.
参考文献 #
Chandrasekhar, S. 1960. Radiative transfer. Dover Publications Inc. #
Cercignani, C. 1988. The Boltzmann Equation and Its Applications. Springer-Verlaq. #
Arvo, J. 1993. Transfer equations in global illumination. SIGGRAPH’93 Course Notes. #
Pauly, M., Kollig, T. and Keller, A., 2000, June. Metropolis light transport for participating media. In Eurographics Workshop on Rendering Techniques (pp. 11-22). Springer, Vienna. #
Jensen, H.W., 2001. Realistic image synthesis using photon mapping. AK Peters/crc Press. #
Hoffman, N. and Preetham, A.J., 2002, March. Rendering outdoor light scattering in real time. In Proceedings of Game Developer Conference (Vol. 2002, pp. 337-352). #
Mishchenko, M.I., 2002. Vector radiative transfer equation for arbitrarily shaped and arbitrarily oriented particles: a microphysical derivation from statistical electromagnetics. Applied optics, 41(33), pp.7114-7134. #
Wenzel, C., 2007, March. Real-Time atmospheric effects in games revisited. In Game Developers Conference (pp. 551-556). #
Wrenninge, M. and Zafar, N.B., 2011. Production Volume Rendering 1: Fundamentals. ACM, New York, NY, USA, ACM SIGGRAPH. #
Wronski, B., 2014, August. Volumetric Fog: Unified Compute Shader-Based Solution to Atmospheric Scattering. In ACM SIGGRAPH. #
Hillaire, S., 2016, July. Physically based sky, atmosphere and cloud rendering in frostbite. In ACM SIGGRAPH. #
Fong, J., Wrenninge, M., Kulla, C. and Habel, R., 2017. Production volume rendering: Siggraph 2017 course. In ACM SIGGRAPH 2017 Courses (pp. 1-79). #
Novák, J., Georgiev, I., Hanika, J., Krivánek, J. and Jarosz, W., 2018, August. Monte Carlo methods for physically based volume rendering. In SIGGRAPH Courses (pp. 14-1). #
Raab, M., 2019. Ray Tracing Inhomogeneous Volumes. In Ray Tracing Gems (pp. 521-531). Apress, Berkeley, CA. #
Guo, Y., Jarabo, A. and Zhao, S., 2021. Beyond mie theory: systematic computation of bulk scattering parameters based on microphysical wave optics. ACM Transactions on Graphics (TOG), 40(6), pp.1-12. #
-
要するに, Volume Rendering 方程式の解の Neumann 級数展開[ Pauly et al. 2000] について, 入射光と媒質が局所的に一様とした場合に得られる漸化式について書きます. ↩︎
-
正確には, Radiative Transfer 方程式 [ Chandrasekhar 1960] から時間依存性を除き, 媒質の光の放射を黒体輻射に限らないとしたものを, この記事では Volume Rendering 方程式と呼びます. 時間依存性を除くのは, 日常の風景のシミュレーションをする用途で, 光の速度を無限と考えて良いと仮定するからです. 光の放射を黒体輻射に限らないとするのは, 蛍光放射や, ゲームの魔法発動時のエフェクトなど, 一般の発光現象を扱いたいからです. ↩︎
-
Radiative Transfer 方程式 [ Chandrasekhar 1960] は, 光の粒子的性質に着目する場合は Boltzmann 方程式から [ Cercignani 1988] , 波動的性質に着目する場合は Maxwell 方程式から [ Mishchenko 2002] [ Guo et al. 2021] 導かれます. 両者とも, 散乱体による光の散乱問題を取り扱うのは共通ですが, 光を粒子として扱うか, 電磁波として扱うかが違います. ↩︎
-
光の波動的性質を無視して, その運動が気体分子運動論で近似できる場合のみ考えます. 屈折率による進行方向の変化も無視します. そして, 媒質粒子との相互作用の際に起こる量子効果は, 散乱係数や位相関数に隠蔽されるものとします. ↩︎
-
光子とその英語名であるフォトンは、一般的に 電磁場の量子のことを指します. この記事では, パストレーシングの分野で言及されるフォトンマッピング[ Jensen 2001]と無矛盾に話を進めたいため, 光子の集団をフォトンと呼びます. ↩︎
-
この記事では source 項へなんでも入れられるよう, 単に \(S\) と書いています. ただし特別な理由が無ければ, 吸収と放出のバランスが取れるように \(S=\mu_aL_{\text{emission}}\) などと吸収係数 \(\mu_a\) を使って書くのが無難です. ↩︎
-
\(\left(\bm{\omega}\cdot\nabla\right)L\left(\bm{x},\bm{\omega}\right) = \left(\frac{d\bm{x}(s)}{ds}\cdot\nabla\right)L\left(\bm{x}(s),\bm{\omega}\right) = \frac{dL\left(\bm{x}(s),\bm{\omega}\right)}{ds}\) ↩︎
-
\(\frac{dy(x)}{dx}+p(x)L(x)=q(x)\) の一般解は \(y(x)=ce^{-\int^x p(\xi)d\xi}+ \int^x q(\zeta)e^{-\int^x_\zeta p(\xi)d\xi}d\zeta\). 積分範囲を \(0\) から \(x\) とすれば, 積分定数は \(c=y(0)\) となります. ↩︎
-
入門的な文献は [ Raab 2019] を, 詳細は [ Fong et al. 2017] [ Novák et al. 2018] を参照してください. ↩︎
-
Boltzmann 方程式から Radiative Transfer 方程式を導くとき, 既に散乱媒質の分布が時間変化によって変わらない, すなわち平衡状態であるという仮定が入っています. ここでは更に, 散乱媒質に対する外場の作用を局所的に無視できるとして, その分布を一様とみなせるとしています. ↩︎
-
さらに例を挙げると, 媒質にミー散乱とレイリー散乱の2種類を, そして光源に平行光 \(L_{\text{sun}} \delta(\bm{\omega}'-\bm{\omega}_{\text{sun}})\) を考え, 内部散乱項でその単一散乱のみを計算するとしたとき, [ Hoffman and Preetham 2002] の Implementation Note にあるモデルが得られます. ↩︎
-
視点から奥に向かって行う計算を紹介するのは, transmittance が 1 になったら計算を打ち切るなど, 実用上の利点があるからです. ↩︎