Walk on Spheres について
December 30, 2022
これは レイトレ Advent Calendar 2022 の記事です.
はじめに #
透明な容器に薄めた牛乳を入れ, 懐中電灯で照らすことで簡易ランタンを作る技があります.


ぼんやりと光る牛乳をパストレーシングで描きたいとき, 単純にはランダムウォークする経路に沿って, ボリュームレンダリング方程式を評価することが考えられます. それほど計算コストをかけたくない場合は, ボリュームレンダリング方程式の拡散近似から, てきとうな近似式を作ることがあるかもしれません.
光に限らず, 熱や電荷など何かが媒質の中に拡散する現象はありふれたものです. 一般の拡散現象に応用できるような, ランダムウォークと 拡散方程式を対応付ける基盤として, Feynman-Kac の公式が知られています [ 江沢 and 中村. 2020].
今年, Feynman-Kac の公式とボリュームレンダリング方程式の類似性から, ボリュームレンダリングの手法 [ Novák et al. 2018] を応用することによって, 空間的に非一様な係数を持った 楕円型偏微分方程式を効率よく解く手法が提案されました [ Sawhney et al. 2022]
この記事では, 楕円型偏微分方程式の最も簡単な場合である Laplace 方程式を取り上げ, その手法の基礎となる Walk on Spheres アルゴリズムを実装することを目標にします.
Dirichlet 境界値問題 #
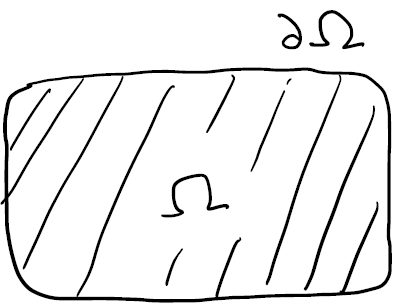
\(d\) 次元空間の中の領域 \(\Omega\) とその境界 \(\partial\Omega\) について, 以下の関数 \(u(x)\) を考えます. \[\left\{ \begin{array}{ll} \frac{1}{2}\Delta u(x) = 0 & x\in\Omega\\ u(x) = g(x) & x\in\partial\Omega \tag{1} \end{array} \right.\] ここで \(\Delta u=0\) は Laplace 方程式と呼ばれ, Laplace 方程式を満たす \(u\) は調和関数と呼ばれています. そして, 境界で \(u\) が何かしらの関数 \(g\) の値となることを課す条件は Dirichlet 境界条件と呼ばれています.
このように, Dirichret 境界条件の下で調和関数 \(u\) を求める問題 (1) を, Dirichlet 境界値問題といいます.
さきほどの牛乳内の光拡散で例えると, 容器のふち \(\partial\Omega\) に光源 \(g(x)\) を置いたときに, 牛乳内 \(\Omega\) へ広がる光拡散 \(u(x)\) を計算する問題に対応します.
Walk-on-Spheres アルゴリズム #
次に, 角谷の原理と, 調和関数の平均値の性質について簡単に触れ, Walk-on-Spheres アルゴリズムの概要の説明へ進みます.
角谷の原理 #
1ステップの移動幅が無限に小さいランダムウォークを, ブラウン運動と呼びます. ここで, \(x\) から出発してブラウン運動によって到着した境界上の点を \(W_\tau\) と書きます.
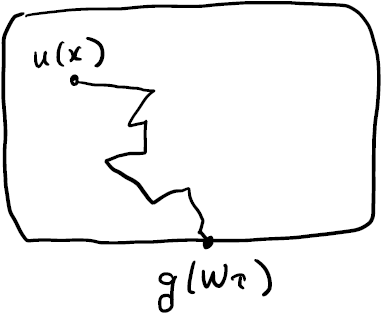
角谷の原理によれば, Dirichlet 境界値問題の解 \(u(x)\) は, \(x\) から出発したブラウン運動で到達した境界の値 \(g(W_\tau)\) の期待値で表されます.
\[\begin{aligned} u(x)=\mathbb{E}\left[g(W_\tau)\right] \tag{2} \end{aligned}\]“角谷の原理” という名前は一般的な呼称ではないようですが, この記事では [ Sawhney et al. 2022] に倣ってそう呼びます. より一般的な偏微分方程式に対する表現については Feynman-Kac の公式を参照してください.
平均値の性質 #
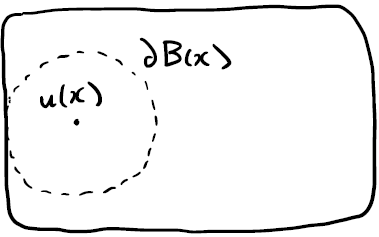
点 \(x\) を中心とする球の球面を \(\partial B(x)\) と書いたとき, 調和関数 \(u(x)\)の値は \(\partial B(x)\) 上の平均値で与えられます.
\[\begin{aligned} u(x) = \frac{1}{|\partial B(x)|}\int_{y\in\partial B(x)}u(y)dy \tag{3} \end{aligned}\] ここで, \(|\partial B|\) は球面の面積です.
Walk-on-Spheres アルゴリズム #
平均値の性質 の積分を, モンテカルロ積分で解くことを考えます. 乱数を使って球面 \(\partial B(x)\) に対して一様に点を \((x^{(1)}, x^{(2)}, \dots, x^{(N)})\) と \(N\) 個生成したとき, (3) の積分は以下のように見積もることができます. \[\begin{aligned} \hat{u}(x) = \frac{1}{N}\sum_{i=1}^N \hat{u}(x^{(i)}) \tag{4} \end{aligned}\] ここで, モンテカルロ積分による推定値を \(\hat{u}\) と表記しました.
上式の \(\hat{u}(x^{(i)})\) がランダムウォークで到着した境界上の点での値になっていれば, 角谷の原理より, 解 \(u(x)\) が近似的に求まります.
Walk-on-Spheres アルゴリズムでは, 球の半径を境界への最近接距離として, 境界へ至るまで球面上に一様に生成した点をランダムに辿ることを考えます. ランダムに辿る球面の順番を \(k\), それぞれの球面上で選んだ点を \(x_k\) と改めて書くと, \(\hat{u}(x_k)\) は以下の漸化式で評価できます.
\[\hat{u}(x_k):= \left\{ \begin{array}{ll} \hat{u}(x_{k+1}) & x_k\in\Omega\\ g(\bar{x}_k) & x_k\in\partial\Omega_\epsilon\\ \tag{5} \end{array} \right.\]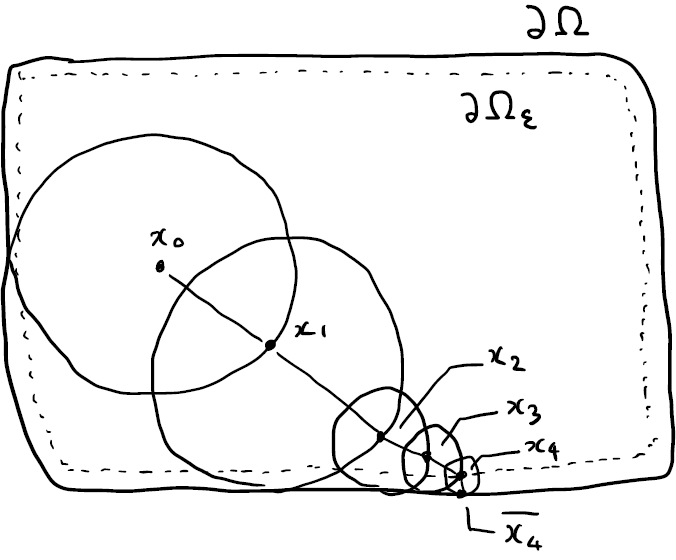
なお, ランダムウォークを有限回で打ち切るために, \(x_k\) と境界上の最近接点 \(\bar{x}_k\) の間の距離が \(\epsilon\) 以下であれば, 境界に達したとみなします. そして, 本来の境界 \(\partial\Omega\) より \(\epsilon\) だけ離れた境界を \(\partial\Omega_\epsilon\) と書きます.
この漸化式 (5) によって, \(x^{(i)}=x_1^{(i)}\) から出発して \(\bar{x}_k\) に到達したランダムウォーク \(W^{(i)}_\tau\) で境界の値が \(g(W^{(i)}_\tau)\) と得られたとすれば, (4) は
\[\begin{aligned} \hat{u}(x) = \frac{1}{N}\sum_{i=1}^N g(W_\tau^{(i)}) \tag{6} \end{aligned}\]と書けます.
実装 #
前節の議論から,
- (5)式: 球面上にランダムに生成した点を境界に至るまで辿り, 境界での値 \(g(W^{(i)}_\tau)\) を求める
- (6)式: \(g(W^{(i)}_\tau)\) の算術平均をとる
とすれば, Dirichlet 境界値問題 (1) を数値的に解くことができることがわかりました.
このサンプルとして, 2次元の Dirichlet 境界値問題に対する Walk-on-Spheres を, ShaderToy に実装しました. https://www.shadertoy.com/view/csjXRw
以下に, ひとつの経路の計算と, その算術平均をとる部分を抜粋します.
//------------------------------------------------------------------------
// 1. 球面上にランダムに生成した点を境界に至るまで辿り, 境界での値を求める
//------------------------------------------------------------------------
float WalkOnSphere(in vec2 p)
{
vec2 result = vec2(0.0);
for(int i = 0; i < MAX_STEPS; i++) {
// 境界への最近接距離を得る
result = SDF(p);
float closest_dist = result.x;
// 最近接距離が 0.001 以下ならループを抜ける
if(closestDist < 0.001) {
break;
}
// 半径 closest_dist の円上へランダムに生成した点に移動する
p += closest_dist * RandomInCircle();
}
// 境界の値を取得する
int id = int(result.y);
return BoundaryValue(p, id);
}
//--------------------------------------------------
// 2. 境界での値の算術平均をとる
//--------------------------------------------------
// Walk on spheres のひとつの経路から得た値を取得
float v = WalkOnSphere(pos);
// 過去に得た history との算術平均をとる
outColor = mix(history, vec3(v), 1.0 / numSamples);
結果 #
https://www.shadertoy.com/view/csjXRw で得られた結果です. 左側に解析解, 右側に数値解の結果を並べてあります.

\(N=1\)
Walk-on-Spheres の経路の数 \(N\) がひとつのときは, ノイズだらけの見た目ですが..

\(N=10000\)
経路の数 \(N\) が十分に大きければ, 数値解が解析解に近いことがわかります.
さいごに #
この記事では, [ Sawhney et al. 2022] の入口に当たる内容として Laplace 方程式の Dirichret 境界値問題を取り上げ, Walk-on-Spheres アルゴリズムの実装を行いました.
参考文献では, より一般的な楕円型編微分方程式に対して multiple importance sampling [ Sawhney and Krane 2020] や delta tracking [ Sawhney et al. 2022] といった, パストレーシングの技術が応用されています.
著者による解説動画 https://www.youtube.com/watch?v=bZbuKOxH71o も要点がわかりやすく説明されているため, 詳しい内容に興味のある方は参考にしてください.